It’s hard to imagine what our understanding of the solar system would be like without Earth’s companion moon. After all, the moon’s orbit provides a baseline and a yardstick of sorts that otherwise wouldn’t be readily available for solving cosmic riddles.
For instance, the moon enables astronomers to figure out the mass of our sun.
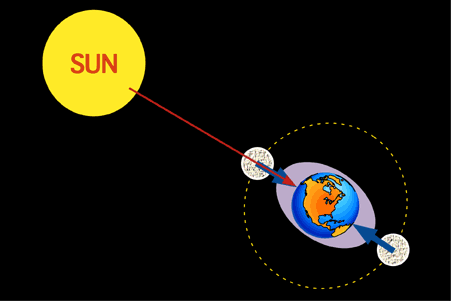
Here’s how you can use our moon – plus any one of the solar system planets of your choosing (including Earth) – to determine the mass of the sun in Earth-masses. Let’s pick the planet Mercury in our example, although any other solar system planet would do the trick as well.
For the task at hand, we need to know the moon’s semi-major axis – mean distance from Earth – and the moon’s orbital period around Earth. Plus, we need to know Mercury’s semi-major axis – its mean distance from the sun – and Mercury’s orbital period around the sun. This information is available in various places, for example this planetary fact sheet from NASA.
Moon’s semi-major axis: 238,855 miles (384,400 km)
Moon’s orbital period: 27.322 Earth-days
Mercury’s semi-major axis: 36,000,000 miles (57,910,000 km)
Mercury’s orbital period: 88 Earth-days
Next, we convert our chosen planet’s semi-major axis and its orbital period into lunar figures:
Mercury’s semi-major axis = 36,000,000/238,855 = 150.719 lunar
Mercury’s orbital period = 88/27.322 = 3.221 lunar
Now … plug these numbers into the equation below to compute the sun’s mass, whereby a = Mercury’s semi-major axis = 150.719 lunar, and p = Mercury’s orbital period = 3.221 lunar:
Sun’s mass = a3/p2
Sun’s mass = a x a x a/p x p
Sun’s mass = 150.719 x 150.719 x 150.719/3.221 x 3.221
Sun’s mass = 3,423,770/10.375 = 330,002 Earth-masses
Technically speaking, the answer of 330,002 is in reference to the Earth-moon system, not the Earth itself. However, since the Earth makes up nearly 99% of the mass of the Earth-moon system, we can be assured that our answer is reasonably close to correct.
You can always double-check your answer by computing the sun’s mass with the moon and another planet. Simply go to the planetary fact sheet to obtain that planet’s semi-major axis and orbital period.
Remember to convert that planet’s semi-major axis (a) and orbital period (p) into lunar figures, and then plug those numbers into the equation: Sun’s mass = a3/p2
Bottom line: How do astronomers figure out the masses of distant stars and planets? Here’s one example – using the moon’s orbit as a baseline to find the mass of our sun – from EarthSky’s Bruce McClure.
Read more:












