Largest known prime number discovered

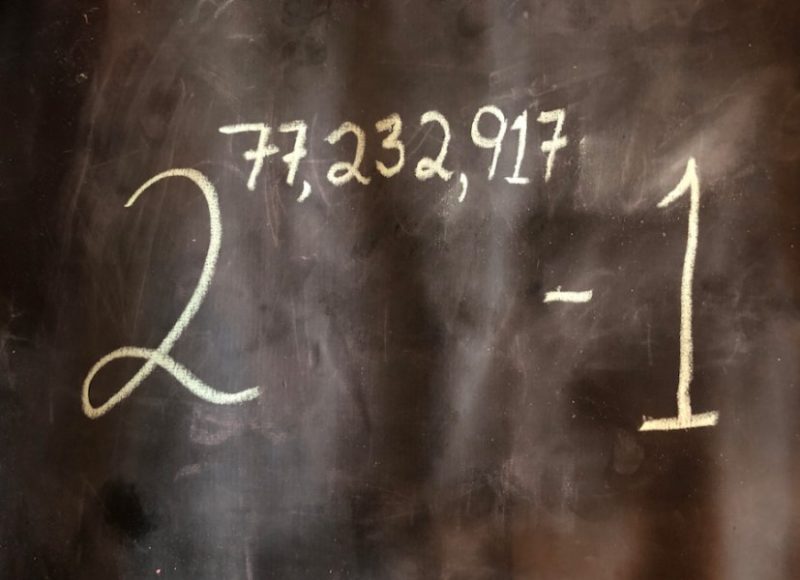
On December 26, 2017, the Great Internet Mersenne Prime Search (GIMPS), a collaborative computer project, discovered the largest known prime number. The number, 2^77,232,917-1, has 23,249,425 digits, nearly one million digits larger than the previous record prime number.

How big is this number? According to a GIMPS statement:

It’s huge!! Big enough to fill an entire shelf of books totaling 9,000 pages! If every second you were to write five digits to an inch then 54 days later you’d have a number stretching over 73 miles (118 kilometers) – almost 3 miles (5 kilometers) longer than the previous record prime.

Jonathan Pace, a 51-year old electrical engineer living in Germantown, Tennessee, made the find. Pace is one of thousands of volunteers using free GIMPS software to search for primes, and has been hunting for big primes with GIMPS for over 14 years.

(Do you want be the next lucky volunteer to discover a brand new largest prime? You’ll need a reasonably modern PC and you can download the free software here. There’s a cash award if your computer discovers a new prime.)

The new prime number, also known as M77232917, is calculated by multiplying together 77,232,917 twos, and then subtracting one. It is in a special class of extremely rare prime numbers known as Mersenne primes. It is only the 50th known Mersenne prime, each increasingly difficult to find. Mersenne primes were named for the French monk Marin Mersenne, who studied these numbers more than 350 years ago. GIMPS, founded in 1996, has discovered the last 16 Mersenne primes.

The primality proof took six days of non-stop computing on a PC. To prove there were no errors in the prime discovery process, the new prime was independently verified using four different programs on four different hardware configurations.

Here’s more information on Mersenne primes, from the GIMPS project

An integer greater than one is called a prime number if its only divisors are one and itself. The first prime numbers are 2, 3, 5, 7, 11, etc. For example, the number 10 is not prime because it is divisible by 2 and 5. A Mersenne prime is a prime number of the form 2P-1. The first Mersenne primes are 3, 7, 31, and 127 corresponding to P = 2, 3, 5, and 7 respectively. There are now 50 known Mersenne primes.

Mersenne primes have been central to number theory since they were first discussed by Euclid about 350 BC. The man whose name they now bear, the French monk Marin Mersenne (1588-1648), made a famous conjecture on which values of P would yield a prime. It took 300 years and several important discoveries in mathematics to settle his conjecture.

At present there are few practical uses for this new large prime, prompting some to ask “why search for these large primes”? Those same doubts existed a few decades ago until important cryptography algorithms were developed based on prime numbers. For seven more good reasons to search for large prime numbers, see here.

Euclid proved that every Mersenne prime generates a perfect number. A perfect number is one whose proper divisors add up to the number itself. The smallest perfect number is 6 = 1 + 2 + 3 and the second perfect number is 28 = 1 + 2 + 4 + 7 + 14. Euler (1707-1783) proved that all even perfect numbers come from Mersenne primes. The newly discovered perfect number is 277,232,916 x (277,232,917-1). This number is over 46 million digits long! It is still unknown if any odd perfect numbers exist.

Bottom line: A new largest prime number, the 50th Mersenne prime, was discovered on December 26, 2017.

Read more from the GIMPS project