Stellar magnitude: An ancient system
When you hear the word magnitude in astronomy, you’re usually hearing a number describing how bright a star – or other space object – looks. The magnitude scale in astronomy is how astronomers categorize differences in brightness among the stars in our sky.
And that scale used by astronomers – the magnitude scale – dates back a long way. The early astronomers Hipparchus (c.190 – c.120 BCE) and Ptolemy (c.100 – c.170 CE) used this scale. Both men compiled star catalogs that listed stars by their apparent brightnesses, or magnitudes.
This system remains intact to this day, though with some modifications.
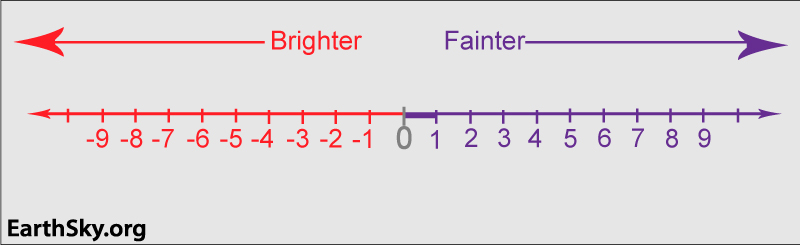
And maybe – to us today – that’s why the magnitude scale doesn’t seem as simple as it might be. According to this ancient scale, the brightest stars in our sky are 1st magnitude. And the very dimmest stars visible to the eye alone are 6th magnitude.
So, a 2nd-magnitude star is modestly bright. But it’s fainter than a 1st-magnitude star.
And a 5th-magnitude star is still pretty faint. But it’s brighter than a 6th-magnitude star.
So, the magnitude scale in astronomy is a lot like a score in golf, in that the lower number means a greater brightness on the magnitude scale (and a better score in golf).
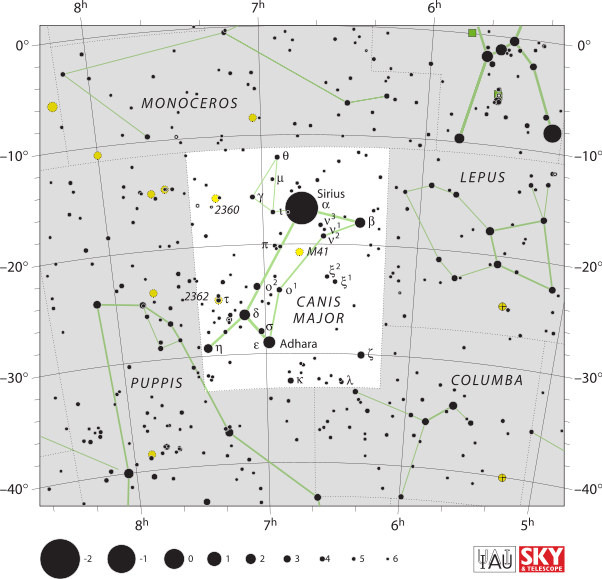
1st-magnitude stars, like Spica
In the spirit of Hipparchus and Ptolemy, the modern-day charts of the constellation Canis Major above and the constellation Virgo below scale stars by magnitude. So, on star charts, the bigger the dot, the brighter the star.
Take the star Spica, the sole bright star in Virgo. It serves as a prime example of a 1st-magnitude star.
In other words, although Spica’s magnitude is slightly variable, its magnitude almost exactly equals 1.

Stars and planets brighter than Spica
Loosely speaking, the 21 stars that are brighter than magnitude 1.50 are called 1st-magnitude stars.
So, the 0-magnitude star Vega (magnitude = 0.00) is actually one magnitude brighter than Spica (m = 1.00).
And the star Sirius with a negative magnitude (m = -1.44) is nearly 2 1/2 magnitudes brighter than Spica.

One magnitude = 2.512 times brighter
Modern astronomy added precision to the magnitude scale. A difference of 5 magnitudes corresponds to a brightness factor of a hundredfold. So, a 1st-magnitude star is 100 times brighter than a 6th-magnitude star.
Or, conversely, a 6th-magnitude star is 100 times dimmer than a 1st-magnitude star.
So, a difference of 1 magnitude corresponds to a brightness factor of about 2.512 times.
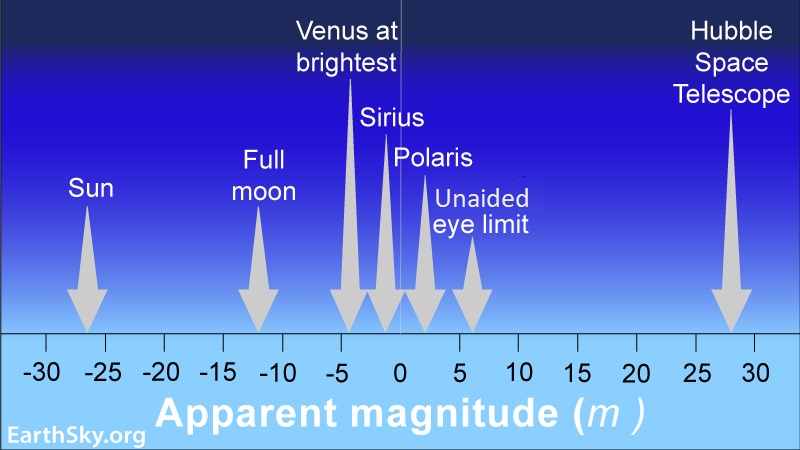
Extending the magnitude scale
The sun and moon, plus the planets Venus and Jupiter, are much, much brighter than 1st magnitude. And modern telescopes let us see stars that are millions of times fainter than 6th magnitude.
Nowadays, the magnitude system includes not just stars but also the moon, planets, asteroids and comets within the solar system. As well as, star clusters and galaxies that reside outside the solar system. Astronomers even list the magnitudes of human-made satellites circling our planet.
Because a difference of 5 magnitudes corresponds to a brightness factor of 100 times, then a difference of 10 magnitudes corresponds to a brightness factor of 10,000 times (100 x 100 = 10,000). In addition, a difference of 15 magnitudes corresponds to a brightness factor of 1,000,000 times, and a difference of 20 magnitudes corresponds to a brightness factor of 100,000,000 times. Hipparchus and Ptolemy would be amazed!
Bottom line: Stellar magnitude is a measurement of brightness for stars and other objects in space.











